This is a Wix version of Time University.

Numbers and Spaces
Single Value Numbers
Numbers that sit on a number line might be considered as having one value.
These one dimensional values are the usual thikngs we thoink of as numbers.
Multi Value Numbers

Complex Numbers are an example of "numbers" that have more than one vale.
Complex numbers are drawn on a 2D plane. This suggests that positions on a plane can be be called "numbers". Numbers might be thought of as things that we can do "operations" such as add or multiply. I.e. Things that we manipulate with "algebra".
Accordonhg to Roger Penrose quaternions are easy to work with algebraicly but anything bigger than octonions get to awkward.



Structures and Spaces

Kevin Carlson sugested "structures" are places we do algebra, and "spaces" as places we do geometry.
Some might suggest that any structure might be imagined as some kind of geometry.
Some logic gates can be thought of as different types of rotations. E.g. Rotations of a Bloch sphere.
Clifford Algebra and Hilbert Space are not usually called Clifford Space and Hilbert Algeba. Likewise, Quantum Mechanics and Quantum Logic are more often talked about than Quantum Algebra. Some of these distinctions may be largely convention. If you see the term Clifford Space on this site, it would llikely be much the same idea as Clifford Algebra. The word "number" on this site may refer at times to any data structure. E.g. a list of names of teddy bears might be thought of as a single number, but the algebraic rules on collections of teddy bear names may differ greatly from algebraic rules of vectors of scalar numbers.

Chosing Numbers, Spaces and Operations

Computer programmers select or design data types to hold data.
These may be lists, vectors, matricies orany set of boxes to hold numbers.
Mathematicians do similar things and have things like spinors and twistors as well as the common real, boolean and integers seen in programming.
All these things might be thought of as different types of numbers sitting in an algebraic space. Even if mer humans have a hard time imagining a piece of computer code or algebra as a geometric transformation, it still might be given enough imagination.
If you were trying to create a type of number or data object similar to a Bloch Sphere but where false = -1 instead of being associated with zero. As a first guess we might try using something like unit vectors or quaternions, but as we explore the concept we may find something in Clifford Algebra that suits better. Similarly we are looking for a type of number that had the property that one more than the largest number rotates around to give the smallest. Modular numbers are a commonly used data type that fits this description but not all of the algebraic properties of modular numbers may fit with the prpoperties we are seeking to emulate. Selecting a well researched data or number type makes finding what things can be done with these numbers much easier than trying to create a algebra from scratch.
Lee Smolin was stuck in his Quantum Gravity reserarch until someone suggested using algebra related to strings and knots. Loop Gravity and String Theory both use counting knots in strings as a way to do math. Quantum Field Theory tries to look at objects similar to grass leaves blown by wind currents. Usually algebras have an analogy or geometry associated with them but not always.
Sometimes Quantum Mechanics can be counter to intuition and people say "shut up and calculate".

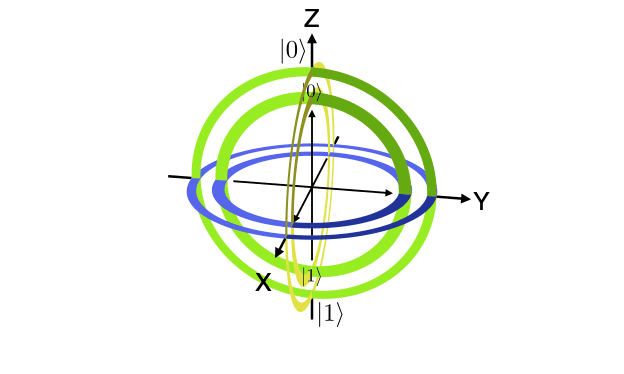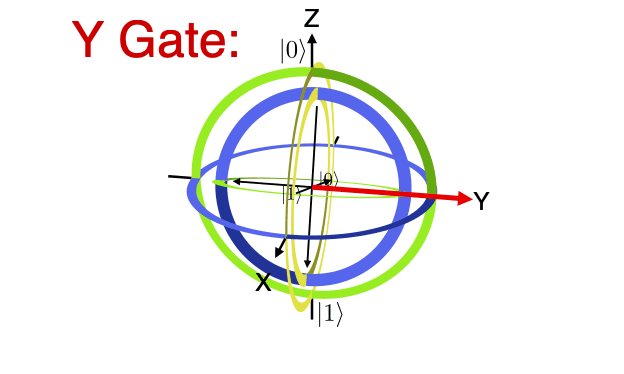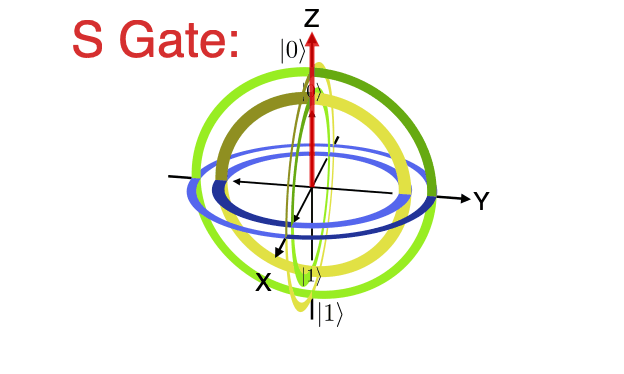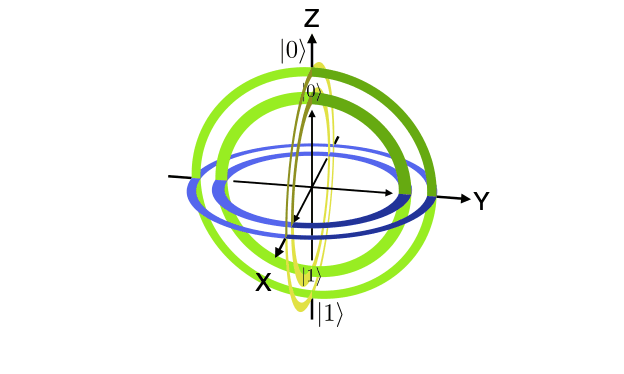
Bloch Spheres can be imagined as a three layered gyroscope or three positions on a sphere. Using a single sphere with a label may make modeling all the aspects of a Bloch Sphere difficult or the different views of the ball may be unique for the same number of orientations. One of the rotations may be modelled by the orientation of the label. Extra complexity might be added by views from inside the sphere as well as outer views.
Physical Objects as Nunbers or data types

Mathematicians often use spheres to describe quantum states or quantum bits. The Bloch Sphere is most commonly used but Reimann and other types of spheres are also used. e.g. when seeking spacetime aspects of quantum data.
One might imagine a ping pong ball with a tick on one side as an concrete analogy for a quantum bit.
We might then decide which algebraic structure or geometric space these balls are placed in.

Quaternions are a commonly used "number" used to model rotations in space navigation and computer graphics.
We might use Quaternions sitting in a Hilbert Space to model our tick labelled balls. Unless there is a known mapping from Bloch Spheres to Quaternions modeling quantum states may require some tweaking.
We might try placing our balls on something mathematically similar to Spacetime Event Horizons.

Whether we use Spinors, Quaternions or Vector related object in Clifford Algebra, we may need rules about the space these objects interact in. This spin-net sits in a conformal space where angles remain set but spacial distances, areas and volumes may be arbitrary and change for different observer viewpoints.
On the other hand we might use a space similar to Minkowski Spacetime where distances in 4D remain the same but projections on to 3D differ.
Whatever system one uses or develops may need to be self consistent and precise.


